Все про квадратні рівняння

Квадратні рівняння є різновидом рівнянь другого степеня з однією змінною. Числа  — його коефіцієнти, при чому  також називається першим коефіцієнтом,  — другим,  — вільним членом. Будь-яке квадратне рівняння має

• або два різних дійсних корені,
• або два однакові дійсних корені (тобто, по суті, один),
• або взагалі не має дійсних коренів, а має два комплексні корені.

(Зазвичай, коли кажуть, що коренів немає, то мається на увазі, що немає дійсних коренів: в такому разі обидва корені є комплексними. Вони позначаються як  та  або, якщо йдеться про обидва корені одночасно, то  В деякій літературі зустрічається ще й таке позначення:  і .) Існують повні, неповні, зведені квадратні рівняння.

Історія розв'язування рівнянь другої степені, в тому числі й квадратних, у стародавні часи була викликана потребою вирішувати проблеми пов'язані з поділом землі, знаходженням її площі, земельними роботами військового характеру, а також із розвитком таких наук, як математика й астрономія. Квадратні рівняння вміли вирішувати вавилоняни близько 2000 років до н.е. Серед клинописних текстів були знайдені приклади розв'язання неповних, а також часткових випадків повних квадратних рівнянь. Відомо, що їхні методи розв'язання майже збігаються із сучасними, проте невідомо, яким чином вавилоняни дійшли до цих методів: майже на всіх знайдених до того часу клинописних текстах збереглися лиш вказівки до знаходження коренів рівнянь, але не вказано, як вони були виведені. Однак, не зважаючи на розвинутість математики у ті часи, в цих текстах немає ані найменшої згадки про від'ємні числа і про загальні методи розв'язання рівнянь.

В стародавній Греції квадратні рівняння розв'язувалися за допомогою геометричних побудов. Методи, які не пов'язувалися з геометрією, вперше наводитьДіофант Александрійський у ІІІ ст. У своїх книгах «Арифметика» він наводить приклади розв'язування неповних квадратних рівнянь. 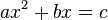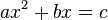Його книги з описом способів розв'язання повних квадратних рівнянь до нашого часу не збереглися.Правило знаходження коренів рівняння, зведеного до вигляду  уперше дав індійський вчений Брахмагупта. Аль-Хорезмі  описав алгоритм для знаходження коренів всіх шести підвидів квадратного рівняння.

Загальне правило розв'язання квадратних рівнянь було сформоване німецьким математиком М. Штифелем (1487 — 1567). Виводом формули загального розв'язку квадратних рівнянь займався Франсуа Вієт. Він же й вивів формули залежності коренів рівняння від коефіцієнтів у 1591 році. Після праць нідерландського математика А. Жирара (1595 — 1632), а також Декарта і Ньютона спосіб розв'язання квадратних рівнянь набув сучасного вигляду.